Don’t confuse precision with accuracy!

These were the words that popped out at me during an excellent presentation by Alex Brown of Xilinx during his keynote presentation. Recently my colleague covered an interview with Alex and it reminded me of his aptly titled presentation “Taming Complexity”. As a practice Supply Chain Management is made up of a bunch of engineers who pride themselves in their mathematical skills, and Alex, with a PhD in Industrial Engineering from Stanford University, is a prime example. Nothing pleases us as much as solving complex problems using mathematics. We spend years learning about linear programming and the theory of optimization, so we want to put these skills into action. What we don’t get taught at university, is that most “interesting” problems are too complex to be solved using mathematics. Recognize that word “complex”? It was in Alex’s title. What we are taught at university is the word “intractable”.

            Most real world problems are intractable, which we don’t get taught at university. What amuses me about the definition is that it’s almost like the problem is being deliberately obdurate, another lovely big word, frustrating the human being.

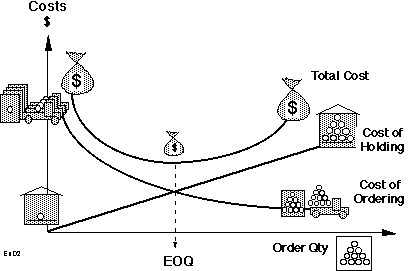
          The reality is that our mathematics isn’t strong enough to deal with the real world. The problems are simply too complex. So we are taught to break up the problem into a lot of smaller pieces, each one of which is tractable, meaning the resultant equations can be solved using “simple” mathematics. But in doing so we have lost the overarching context, and therefore we are not solving the real problem. We have simplified the original problem beyond recognizability. We forget the difference between teaching a method and applying that method to real world problems. Alex addressed one aspect of this issue during his presentation when he discussed the Economic Order Quantity calculation, a classic of all Industrial Engineering and Operations Research courses. It is meant to show the use of optimization techniques to set the standard quantity of material to be ordered and is based upon balancing the cost of ordering against the cost of holding inventory. Order larger amounts infrequently and the cost of ordering goes down, but the cost of holding inventory goes up. Order small amounts frequently and the cost of ordering goes up, but the cost of holding inventory goes down. I love the diagram below, which I found on the internet. The icons are particularly helpful, in case the problem has not been simplified sufficiently.

              Source: https://ais.web.cern.ch/ais/apps/lims/images/EXCEPT~1convert2.gif

Alex’ point is that if you collect all the information and use the equations to calculate the EOQ (there are even some website that do this for you) the result will show that you need to order 98.325752. As Alex said, in reality is doesn’t make much difference if you order 80 or 120. This is confusing precision with accuracy. There are three problems with the equation which lead to Alex’ assertion that the answer lies in the 80-120 range, and that we cannot be more precise than that. The first is the simplicity of the equation, the second is the accuracy of the input data, and the third is variability or uncertainty. I will discuss these three problems collectively because, and this is the fourth problem, they are interlinked and cannot be separated out. But let me pause before diving into a deeper discussion to state that using the EOQ equation to determine how much to order is far, far better than simply guessing how much to order. But let us recognize it for what it is: A simplistic answer to a complex problem. Let us start by addressing the simplicity of the equation. What is ignored is that the company may be buying several items from the same supplier and therefore it is cheaper to have several items delivered together, because doing so reduces the transportation costs. Notice that the EOQ equation does not even consider the cost of transportation because it assumes it is a constant regardless of the quantity purchased. It also ignores the purchase price, assuming that there is no bulk purchase discount. I would argue that both are gross simplifications. There is always variability in the demand signal and in the lead time for delivery, both of which lead to safety stock. While it is true that the EOQ equation captures the variable cost of purchasing more or less, having more safety stock because of variability will flatten the total cost curve meaning that the relative difference between different order quantities will have an even smaller effect. The diagram below shows the impact on the amount of safety stock where the % values represent the amount of safety stock as a percentage of the average stock over the ordering period. This % will depend on the variability of the demand and supply lead times. As we can see, the EOQ decreases as the relative amount of safety stock increases. Of course the exact shape of the curve will depend on the relative values of the variables used in the equation, but the overall principle will remain the same.

Of course in this example we are only considering one item at one location. What if this is a multi-echelon distribution network? And what if the supplier could deliver from more than one location, perhaps at the same price, but with a different lead time? We can see that the traditional EOQ equation is a gross simplification of the real world, but that it was approximately correct. In other words, do not confuse accuracy with precision. The simple EOQ equation produces a result that is more right than wrong, making it extremely useful. But if you think it provides a result that is more than 80% correct you are wrong. I had a recent discussion with a customer that is thinking of using Kinaxis RapidResponse for demand planning, but was getting pushback from the demand planning team because we do not support the Lewandowski method. Let us put this into perspective. Independent studies show that best in class forecast accuracy in weekly buckets, by customer and item, at lead time is around 70%, while the typical forecast accuracy is no more than 60%. Of course these forecast accuracy measures go up as the time bucket and as we go up the product or customer hierarchies. The point being that it is the forecast accuracy at customer and site that actually matters because this is what determines production and distribution schedules. Our customer, while being recognized by Gartner as one of the Top 25, is no different. Their forecast accuracy falls into the bands above, despite using Lewandowski. On the other hand using simpler, more easily configured and understood forecasting methods will have limited impact on their forecast accuracy. This can be proven. So once again, do not confuse precision with accuracy. What matters far more in terms of their ability to meet customer demand with a reasonable profit is an agile supply chain. Of course they can’t be hopelessly wrong in their forecast otherwise they will need a lot of inventory and would still have poor customer service, ultimately leading to lost profitability and revenue. But, far more important than the precise forecast for a period are questions about trends and mix changes. These have a much greater impact on the agility of the supply chain and its consequent ability to absorb demand variability. Are you fighting core complexity at your organization? If so, comment below and let us know.